网上对hash表的介绍和总结有很多,但看完了总感觉不是自己的。所以自己总结了hash表,形成自己的知识图表,也希望能够对自己和大家有些帮助。
哈希表(Hash table,也叫散列表),是根据关键字(Key value)而直接进行访问的数据结构。
大学时学过数据结构,不过基本都忘了,而且那时候刚刚编程,对数据结构也没多大印象,所以现在需要补起来了。
hash的英文意思[n. 剁碎的食物;混杂,拼凑;重新表述,vt. 搞糟,把…弄乱;切细;推敲]
hash表也叫哈希表,散列表,hash table,hash表,以后看见这几个记得都是一个意思。
hash函数也叫哈希函数,hash函数,散列函数,也都是一个意思。
1. 定义
哈希表是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
哈希函数给定表M,存在函数f(key),对任意给定的关键字值key,代入函数后若能得到包含该关键字的记录在表中的地址,则称表M为哈希(Hash),函数f(key)为哈希(Hash) 函数(也叫散列函数)。
对上面的意思白话解释:结合图1 hash表解释,图中的key就是关键字,就是存在一个固定大小的数组,这个数组就是散列表,这个数组中放的数据是有特点的,可以形象的想成key-value形式,value可以是自己自身或其他数据。如果要正常访问数组中的数据,需要用查找的key和数组中的key一个个比较,这样访问速度不是很慢吗,那么是否我可以把key和value形成某种关系对应起来呢,比如通过函数address=f(key),这个address就是数组中的位置,这样我就不需要比较直接通过array[index]直接就访问了,这样访问速度就很快了。所以address=f(key)这个函数就叫哈希(Hash)函数(也叫散列函数)了。
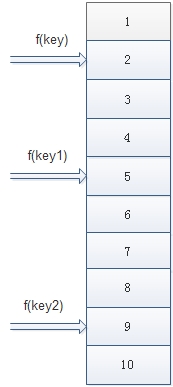
一般的线性表,树中,记录在结构中的相对位置是随机的,即和记录的关键字之间不存在确定的关系,因此,在结构中查找记录时需进行一系列和关键字的比较。这一类查找方法建立在“比较“的基础上,查找的效率依赖于查找过程中所进行的比较次数。 理想的情况是能直接找到需要的记录,因此必须在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使每个关键字和结构中一个唯一的存储位置相对应。
2. 基本概念
理解哈希表需要涉及到一下几个概念
若关键字为k,则其值存放在f(k)的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系f为散列函数,按这个思想建立的表为散列表。
散列函数有下面的特点- 两个相等的对象值他的散列函数的结果一定是相等的。
- 上面的结果反过来是不一定成立的,即如果两个对象的值的散列函数的结果相等,那么他们俩的值是不一定相等的。
- 如果两个对象的值的散列函数结果不相等,那么他们的值是一定不相等的。
对不同的关键字可能得到同一散列地址,即k1≠k2,而f(k1)=f(k2),这种现象称为碰撞(英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数f(k)和处理碰撞的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。
- 若对于关键字集合中的任一个关键字,经散列函数映象到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就是使关键字经过散列函数得到一个“随机的地址”,从而减少碰撞。
3. 常用散列函数介绍
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快地定位。
实际工作中需视不同的情况采用不同的散列函数,通常考虑的因素有:
- 计算散列函数所需时间
- 关键字的长度
- 哈希表的大小
- 关键字的分布情况
- 记录的查找频率
通过上面介绍我们知道,决定散列表性能的关键是散列函数和冲突的处理
散列函数设计的好可以很快的定位到存储位置,冲突问题解决的好可以加快hash表的访问速度。下面是常用的散列函数
3.1. 直接寻址法
取关键字或关键字的某个线性函数值为散列地址。即f(key)=key或f(key) = a·key + b,其中a和b为常数(这种散列函数叫做自身函数)。若其中f(key)中已经有值了,就往下一个找,直到f(key)中没有值了,就放进去。
3.2. 数字分析法
分析一组数据,比如一组员工的出生年月日,这时我们发现出生年月日的前几位数字大体相同,这样的话,出现冲突的几率就会很大,但是我们发现年月日的后几位表示月份和具体日期的数字差别很大,如果用后面的数字来构成散列地址,则冲突的几率会明显降低。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
3.3. 平方取中法
当无法确定关键字中哪几位分布较均匀时,可以先求出关键字的平方值,然后按需要取平方值的中间几位作为哈希地址。这是因为:平方后中间几位和关键字中每一位都相关,故不同关键字会以较高的概率产生不同的哈希地址。
例:我们把英文字母在字母表中的位置序号作为该英文字母的内部编码。例如K的内部编码为11,E的内部编码为05,Y的内部编码为25,A的内部编码为01, B的内部编码为02。由此组成关键字“KEYA”的内部代码为11052501,同理我们可以得到关键字“KYAB”、“AKEY”、“BKEY”的内部编码。之后对关键字进行平方运算后,取出第7到第9位作为该关键字哈希地址,如下表所示
| 关键字 | 内部编码 | 内部编码的平方值 | H(k)关键字的哈希地址 |
|---|---|---|---|
| KEYA | 11050201 | 122157778355001 | 778 |
| KYAB | 11250102 | 126564795010404 | 795 |
| AKEY | 01110525 | 001233265775625 | 265 |
| BKEY | 02110525 | 004454315775625 | 315 |
3.4. 折叠法
将关键字分割成位数相同的几部分,最后一部分位数可以不同,然后取这几部分的叠加和(去除进位)作为散列地址。数位叠加可以有移位叠加和间界叠加两种方法。移位叠加是将分割后的每一部分的最低位对齐,然后相加;间界叠加是从一端向另一端沿分割界来回折叠,然后对齐相加。
3.5. 随机数法
选择一随机函数,取关键字的随机值作为散列地址,通常用于关键字长度不同的场合。
3.6. 除留余数法
取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 f(key) = key MOD p,p<=m,此函数等价于f(key) = (key % p),p<=m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要,一般取素数或m,若p选的不好,容易产生同义词。
4. 冲突
无论哈希函数设计有多么精细,都会产生冲突现象,也就是2个关键字处理函数的结果映射在了同一位置上,因此,有一些方法可以避免冲突。
4.1. 拉链法
拉出一个动态链表代替静态顺序存储结构,可以避免哈希函数的冲突,不过缺点就是链表的设计过于麻烦,增加了编程复杂度。此法可以完全避免哈希函数的冲突。
4.2. 多哈希法
设计二种甚至多种哈希函数,可以避免冲突,但是冲突几率还是有的,函数设计的越好或越多都可以将几率降到最低(除非人品太差,否则几乎不可能冲突)。
4.3. 开放地址法
开放地址法有一个公式:Hi=(H(key)+di) MOD m i=1,2,...,k(k<=m-1)
其中,m为哈希表的表长。di是产生冲突的时候的增量序列。如果di值可能为1,2,3,...m-1,称线性探测再散列。
如果di取1,则每次冲突之后,向后移动1个位置.如果di取值可能为1,-1,4,-4,9,-9,16,-16,...k*k,-k*k(k<=m/2)
称二次探测再散列。如果di取值可能为伪随机数列。称伪随机探测再散列。
4.4. 建域法
假设哈希函数的值域为[0,m-1],则设向量HashTable[0..m-1]为基本表,另外设立存储空间向量OverTable[0..v]用以存储发生冲突的记录。
5. 查找性能
散列表的查找过程基本上和造表过程相同。一些关键码可通过散列函数转换的地址直接找到,另一些关键码在散列函数得到的地址上产生了冲突,需要按处理冲突的方法进行查找。在介绍的三种处理冲突的方法中,产生冲突后的查找仍然是给定值与关键码进行比较的过程。所以,对散列表查找效率的量度,依然用平均查找长度来衡量。
查找过程中,关键码的比较次数,取决于产生冲突的多少,产生的冲突少,查找效率就高,产生的冲突多,查找效率就低。因此,影响产生冲突多少的因素,也就是影响查找效率的因素。影响产生冲突多少有以下三个因素:
- 散列函数是否均匀;
- 处理冲突的方法;
- 散列表的装填因子。
散列表的装填因子定义为:α= 填入表中的元素个数 / 散列表的长度
α是散列表装满程度的标志因子。由于表长是定值,α与“填入表中的元素个数”成正比,所以,α越大,填入表中的元素较多,产生冲突的可能性就越大;
α越小,填入表中的元素较少,产生冲突的可能性就越小。
实际上,散列表的平均查找长度是装填因子α的函数,只是不同处理冲突的方法有不同的函数。
6. 一些著名的hash算法(即散列函数)
了解了hash基本定义,就不能不提到一些著名的hash算法,如下:
- MD4:MD4(RFC 1320)是 MIT 的 Ronald L. Rivest 在 1990 年设计的,MD 是 Message Digest 的缩写。它适用在32位字长的处理器上用高速软件实现–它是基于 32 位操作数的位操作来实现的。
- MD5 :MD5(RFC 1321)是 Rivest 于1991年对MD4的改进版本。它对输入仍以512位分组,其输出是4个32位字的级联,与 MD4 相同。MD5比MD4来得复杂,并且速度较之要慢一点,但更安全,在抗分析和抗差分方面表现更好
- SHA-1 及其他:SHA1是由NIST NSA设计为同DSA一起使用的,它对长度小于264的输入,产生长度为160bit的散列值,因此抗穷举(brute-force)性更好。SHA-1 设计时基于和MD4相同原理,并且模仿了该算法。
7. 应用
hash算法应用主要是在安全方面,安全方面的应用如下:
- 文件校验
- 数字签名
- 鉴权协议
7.1. MD5、SHA1的破解
不过现在MD5和SHA-1已经不是很安全了
2004年8月17日,在美国加州圣芭芭拉召开的国际密码大会上,山东大学王小云教授在国际会议上首次宣布了她及她的研究小组的研究成果——对MD5、HAVAL-128、MD4和RIPEMD等四个著名密码算法的破译结果。2005年2月宣布破解SHA-1密码。
如果上面有哪些不对的,欢迎大家指正,在此感谢!
想了解更多技术文章信息,请继续关注wiliam.s Blog,谢谢,欢迎来访!
